分类:函数:修订间差异
来自高中笔记
更多操作
无编辑摘要 |
|||
| (未显示同一用户的12个中间版本) | |||
| 第22行: | 第22行: | ||
=== 函数的本质 === | === 函数的本质 === | ||
* 函数是一种特殊的映射,其中集合 <math>A</math> 和 <math>B</math> 都是数集。 | * 函数是一种特殊的映射,其中集合 <math>A</math> 和 <math>B</math> 都是数集。 | ||
* 函数的对应关系必须满足 | * 函数的对应关系必须满足'''单值性''',即每个 <math>x \in A</math> 只能对应一个 <math>y \in B</math>。 | ||
== 表示方法 == | == 表示方法 == | ||
<del>这是初中笔记吗,怎么还写上表示方法了(?</del> | <del>这是初中笔记吗,怎么还写上表示方法了(?</del> | ||
| 第42行: | 第40行: | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| <math>x</math> || -2 || -1 || 0 || 1 || 2 | | <math>x</math>|| -2 || -1 || 0 || 1 || 2 | ||
|- | |- | ||
| <math>f(x)</math> || 4 || 1 || 0 || 1 || 4 | | <math>f(x)</math>|| 4 || 1 || 0 || 1 || 4 | ||
|} | |} | ||
| 第73行: | 第71行: | ||
* 求值域的方法:观察法、配方法、反函数法、判别式法等 | * 求值域的方法:观察法、配方法、反函数法、判别式法等 | ||
== 函数的奇偶性 == | |||
{| class="wikitable" | |||
|+函数奇偶性的定义 | |||
! | |||
!偶函数 | |||
!奇函数 | |||
|- | |||
|文字语言 | |||
|如果 <math>F(x)</math> 的图像是以 <math>y</math> 轴为对称轴的轴对称图形,就称 <math>F(x)</math> 是偶函数 | |||
|如果 <math>F(x)</math> 的图像是以原点为中心的中心对称图形,就称 <math>F(x)</math> 是奇函数 | |||
|- | |||
|符号语言 | |||
|如果对一切使 <math>F(x)</math> 有定义的 <math>x</math>,<math>F(-x)</math> 也有定义,并且 <math>F(-x) = F(x)</math>,则称 <math>F(x)</math> 为偶函数 | |||
|如果对一切使 <math>F(x)</math> 有定义的 <math>x</math>,<math>F(-x)</math> 也有定义,并且 <math>F(-x) = -F(x)</math>,则称 <math>F(x)</math> 为奇函数 | |||
|- | |||
|定义域特征 | |||
| colspan="2" |定义域必须是关于原点对称的区间 | |||
|} | |||
……↑大概意思就是说: | |||
* <math>F(-x) = -F(x)</math> 就是奇函数; | |||
* <math>F(-x) = F(x)</math> 就是偶函数. | |||
函数按奇偶性分类: | |||
# 奇函数; | |||
# 偶函数; | |||
# 既是奇函数又是偶函数; | |||
# 非奇非偶函数. | |||
2026年1月19日 (一) 15:45的最新版本
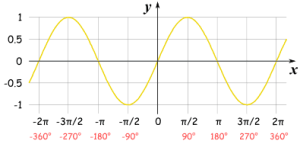
描述自变量与因变量之间的依赖关系。
定义
- 设 是非空的数集,
- 如果对于集合 中任意一个数 ,
- 按照某种确定的对应关系 ,
- 在集合 中都有唯一确定的数 和它对应,
- 那么就称 为从集合 到集合 的一个函数,记作 .
- 叫做自变量,
- 的取值范围 叫做函数的定义域,
- 与 的值相对应的 值叫做函数值,
- 函数值的集合 叫做函数的值域.
函数的三要素
- 定义域
- 对应法则
- 值域
若两个函数的定义域和对应法则相同,则它们是同一函数。
函数的本质
- 函数是一种特殊的映射,其中集合 和 都是数集。
- 函数的对应关系必须满足单值性,即每个 只能对应一个 。
表示方法
这是初中笔记吗,怎么还写上表示方法了(?
解析法
用数学表达式(解析式)来表示函数关系的方法。
- 优点:精确、便于计算和分析。
示例:
列表法
通过列出表格来表示函数的方法,通常用于定义域为有限集的情况。
- 优点:直观、便于查询具体函数值。
示例:
| -2 | -1 | 0 | 1 | 2 | |
| 4 | 1 | 0 | 1 | 4 |
图像法
用平面直角坐标系中的图形来表示函数关系的方法。
- 优点:直观展示函数的变化趋势和性质。
- 图像的定义:函数 的图像是坐标平面上的点集 。
- 函数图像与垂直直线的交点:任意垂直于 x 轴的直线与函数图像至多有一个交点(单值性的几何意义)。
函数的定义域
函数的定义域是自变量 的取值范围,通常由以下因素确定: 1. 解析式有意义的条件(如分母不为零、偶次根号内非负等) 2. 实际问题的限制(如时间、长度等非负) 3. 人为约定的范围
求定义域的步骤
1. 写出解析式有意义的不等式(组) 2. 解不等式(组) 3. 用集合或区间表示解集
示例
- 函数 的定义域为 ,即
- 函数 的定义域为 ,即
函数的值域
函数的值域是函数值的集合,通常由定义域和对应法则共同确定。
- 值域是集合 的子集,即
- 求值域的方法:观察法、配方法、反函数法、判别式法等
函数的奇偶性
| 偶函数 | 奇函数 | |
|---|---|---|
| 文字语言 | 如果 的图像是以 轴为对称轴的轴对称图形,就称 是偶函数 | 如果 的图像是以原点为中心的中心对称图形,就称 是奇函数 |
| 符号语言 | 如果对一切使 有定义的 , 也有定义,并且 ,则称 为偶函数 | 如果对一切使 有定义的 , 也有定义,并且 ,则称 为奇函数 |
| 定义域特征 | 定义域必须是关于原点对称的区间 | |
……↑大概意思就是说:
- 就是奇函数;
- 就是偶函数.
函数按奇偶性分类:
- 奇函数;
- 偶函数;
- 既是奇函数又是偶函数;
- 非奇非偶函数.
