不等式:修订间差异
来自高中笔记
更多操作
| (未显示同一用户的3个中间版本) | |||
| 第65行: | 第65行: | ||
== 一元二次不等式 == | == 一元二次不等式 == | ||
{| class="wikitable" | {| class="wikitable" | ||
|+ | |+与二次函数的关系 | ||
! | ! | ||
!<math>\Delta > 0</math> | !<math>\Delta > 0</math> | ||
| 第75行: | 第73行: | ||
|- | |- | ||
!<math>y = ax^2 + bx + c \quad (a > 0)</math> 的图象 | !<math>y = ax^2 + bx + c \quad (a > 0)</math> 的图象 | ||
|[[文件:Delta大于0.png|缩略图| | |[[文件:Delta大于0.png|缩略图|140px|此时与x轴有两个交点]] | ||
|[[文件:Delta等于0.png|缩略图| | |[[文件:Delta等于0.png|缩略图|140px|此时图像与x轴有且仅有一个交点(或有两个相同的实数解)]] | ||
|[[文件:Delta小于0.png|缩略图| | |[[文件:Delta小于0.png|缩略图|140px|此时与x轴没有交点]] | ||
|- | |- | ||
!<math>ax^2 + bx + c = 0 \quad (a > 0)</math> 的根 | !<math>ax^2 + bx + c = 0 \quad (a > 0)</math> 的根 | ||
| 第94行: | 第92行: | ||
|<math>\emptyset</math> | |<math>\emptyset</math> | ||
|} | |} | ||
== 一元二次方程根的分布/二次函数的零点分布(卡根法) == | |||
{| class="wikitable" | |||
|+两根与 0 的大小比较即根的正负情况(表一) | |||
!分布情况 | |||
!两个负根 即两根都小于 0 | |||
<math>(x_1 < 0, x_2 < 0)</math> | |||
!两个正根 即两根都大于 0 | |||
!一正根一负根 即一根小于 0,一根大于 0 | |||
|- | |||
!大致图象 <math>(a>0)</math> | |||
|<图象> | |||
|<图象> | |||
|<图象> | |||
|- | |||
!得出的结论 | |||
| | |||
| | |||
| | |||
|} | |||
{| class="wikitable" | |||
|+两根与 0 的大小比较即根的正负情况(表二) | |||
!分布情况 | |||
!两个负根 即两根都小于 0 | |||
!两个正根 即两根都大于 0 | |||
!一正根一负根 即一根小于 0,一根大于 0 | |||
|- | |||
!大致图象 (a<0) | |||
|<图象> | |||
|<图象> | |||
|<图象> | |||
|- | |||
!得出的结论 | |||
| | |||
| | |||
| | |||
|} | |||
= 例题 = | = 例题 = | ||
| 第99行: | 第135行: | ||
=== 用一段长为 <math>36\,\text{m}</math> 的篱笆围成一个矩形菜园.=== | === 用一段长为 <math>36\,\text{m}</math> 的篱笆围成一个矩形菜园.=== | ||
# 当这个矩形的边长为多少时,所用篱笆最短?最短篱笆的长度是多少? | # 当这个矩形的边长为多少时,所用篱笆最短?最短篱笆的长度是多少? | ||
# 当这个矩形的边长为多少时,菜园的面积最大?最大面积是多少? | #当这个矩形的边长为多少时,菜园的面积最大?最大面积是多少? | ||
解:设矩形菜园的相邻两条边的长分别为 <math>x\,\text{m}, y\,\text{m}</math>,则篱笆的长度为 <math>2(x + y)\,\text{m}</math>. | 解:设矩形菜园的相邻两条边的长分别为 <math>x\,\text{m}, y\,\text{m}</math>,则篱笆的长度为 <math>2(x + y)\,\text{m}</math>. | ||
2025年12月24日 (三) 02:55的最新版本
我们经常用不等式来研究含有不等关系的问题.
基本事实
如果 , 那么
如果 , 那么
如果 , 那么
反过来也成立. 即
所以,如要证明 , 只需证明 即可.
基本不等式
把不等式 称为基本不等式.
对任意 ,当且仅当 时等号成立.
对任意正数 ,当且仅当 时等号成立.
一般地,对于正数 ,我们把 称为 的算术平均数, 称为 的几何平均数.
拓展结论
- 已知 都为正数,如果 等于定值 ,那么当且仅当 时,和 有最小值 ;
- 如果 是定值 ,那么当且仅当 时,积 有最大值 .
由此可总结出:
当两个正数变量的积或和为定值时,他们的和有最小值或积有最大值
糖水原理
克糖水中有 克糖,
它的质量分数就是 .
再向容器中加入 克糖,
得到质量分数为 的糖溶液.
加入两次糖后的溶液更甜,即后者质量分数更大.
即
.
证明过程
其中,.
作差证明:
所以 .
一元二次不等式
| 的图象 | 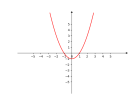 |
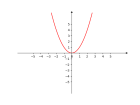 |
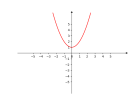 |
|---|---|---|---|
| 的根 | 有两个不相等的实数根 | 有两个相等的实数根 | 没有实数根 |
| 的解集 | |||
| 的解集 |
一元二次方程根的分布/二次函数的零点分布(卡根法)
| 分布情况 | 两个负根 即两根都小于 0
|
两个正根 即两根都大于 0 | 一正根一负根 即一根小于 0,一根大于 0 |
|---|---|---|---|
| 大致图象 | <图象> | <图象> | <图象> |
| 得出的结论 |
| 分布情况 | 两个负根 即两根都小于 0 | 两个正根 即两根都大于 0 | 一正根一负根 即一根小于 0,一根大于 0 |
|---|---|---|---|
| 大致图象 (a<0) | <图象> | <图象> | <图象> |
| 得出的结论 |
例题
基本不等式
用一段长为 的篱笆围成一个矩形菜园.
- 当这个矩形的边长为多少时,所用篱笆最短?最短篱笆的长度是多少?
- 当这个矩形的边长为多少时,菜园的面积最大?最大面积是多少?
解:设矩形菜园的相邻两条边的长分别为 ,则篱笆的长度为 .
1.
- 由已知,得 ,
- 根据基本不等式 ,
- 可得 ,
- 所以,
- 当且仅当 时,上式等号成立.
- 因此,当这个矩形菜园是边长为 的正方形时,所用篱笆最短,最短篱笆的长度为 .
2.
- 由已知,得 ,矩形菜园的面积为 .
- 根据基本不等式可得 ,
- 所以,.
- 当且仅当 时,上式等号成立.
- 因此,当这个矩形菜园时边长为 的正方形时,菜园面积最大,最大面积是 .
