集合:修订间差异
来自高中笔记
更多操作
小 标准化 |
|||
| (未显示2个用户的26个中间版本) | |||
| 第1行: | 第1行: | ||
把研究的对象集在一起构成<strong>集合</strong>. | |||
* 有有限个元素:有限集; | |||
* 有无限个元素:无限集. | |||
=== 空集 === | === 空集 === | ||
不含元素的集合:<math>\emptyset</math> | |||
<strong>空集也是有限集</strong> | <strong>空集也是有限集</strong>. | ||
== 元素和集合的关系 == | == 元素和集合的关系 == | ||
属于:<math>\in</math> | |||
不属于:<math>\notin</math> | |||
== 集合中元素的三个特征 == | == 集合中元素的三个特征 == | ||
# 确定性:给定的集合,它的'''元素必须是确定的'''. 也就是说,给定一个集合,那么任何一个元素是否存在这一个集合中就确定了. | |||
# 互异型:一个给定集合中的'''元素是互不相同的'''. 也就是说,集合中的元素是不重复出现的. | |||
# 无序性:给定集合中的'''元素是不分先后的''',没有顺序的. | |||
== 数集 == | == 数集 == | ||
[[文件:数集.png|200px|缩略图|数集之间的关系(Venn 图)]] | |||
数学里最常用的集合是各种数的集合,简称<strong>数集</strong>。 | 数学里最常用的集合是各种数的集合,简称<strong>数集</strong>。 | ||
| 第35行: | 第29行: | ||
=== 示例 === | === 示例 === | ||
所有正整数组成的集合称为<strong>正整数集</strong>,记作 N* | # 所有正整数组成的集合称为<strong>正整数集</strong>,记作 <math>\mathbb{N}^*</math>,<math>\mathbb{Z}^+</math> 或 <math>\mathbb{N}^+</math> | ||
# 所有负整数组成的集合称为<strong>负整数集</strong>,记作 <math>\mathbb{Z}_-</math> | |||
# 全体自然数组成的集合称为<strong>自然数集</strong>,记作 <math>\mathbb{N}</math> | |||
# 全体整数组成的集合称为<strong>整数集</strong>,记作 <math>\mathbb{Z}</math> | |||
# 全体有理数组成的集合称为<strong>有理数集</strong>,记作 <math>\mathbb{Q}</math> | |||
# 全体实数组成的集合称为<strong>实数集</strong>,记作 <math>\mathbb{R}</math> | |||
== 集合的表示方法 == | |||
=== 列举法 === | |||
把集合中的所有元素'''一一列举出来''',并用花括号“<math>\{ \}</math>”括起来表示集合的方法叫做'''列举法'''. | |||
注意事项: | |||
# 元素与元素之间必须用“<math>,</math>”隔开. | |||
# 集合中的元素可以是任何事物. | |||
# 集合中的元素不能重复. | |||
示例: | |||
一元二次方程 <math>3x^2 - 6x = 0</math> 的解集为:<math>\{0, 2\}</math>. | |||
=== 描述法 === | |||
一般地,设 A 表示一个集合,把集合 A 中所有具有共同特征 P(x) 的元素 x 所组成的集合表示为 <math>\{x \in A | P(x)\}</math>,这种表示方法称为'''描述法'''. | |||
注意事项: | |||
# 写清楚集合中元素的符号. 如数或点等. | |||
# 不能出现未被说明的字母. | |||
示例: | |||
奇数集:<math>\{x | x = 2n + 1, n \in \mathbb{N}\}</math>. | |||
偶数集:<math>\{x | x = 2n, n \in \mathbb{N}\}</math>. | |||
== 子集 == | == 子集 == | ||
'''如果集合 A 的每一个元素都是集合 B 的元素,就称 A 是 B 的一个子集''' | [[文件:真子集.jpg|120px|缩略图|描述 A 真包含于 B 的 Venn 图]] | ||
'''如果集合 <math>A</math> 的每一个元素都是集合 <math>B</math> 的元素,就称 <math>A</math> 是 <math>B</math> 的一个子集'''. | |||
记作 <math>A \subseteq B</math>(读作:'''A 包含于 B''')或 <math>B \supseteq A</math>('''B 包含 A'''). | |||
如果 <math>A \subseteq B</math> 并且 <math>B \subseteq A</math>,就说这两个集合'''相等''',记作:<math>A = B</math>. | |||
如果 <math>A \subseteq B</math> 但是 <math>A \neq B</math>,就说 A 是 B 的'''真子集''',记作:<math>A \subsetneqq B</math>,读作:'''A 真包含于 B'''. 例如,<math>(1, 6) \subsetneqq [1, 6]</math>. | |||
包含关系还有传递性: | |||
# 若 <math>A \subseteq B</math>,<math>B \subseteq C</math>,则 <math>A \subseteq C</math>; | |||
# 若 <math>A \subsetneqq B</math>,<math>B \subseteq C</math>,则 <math>A \subseteq C</math>; | |||
等等. | |||
=== 有限集的子集个数的确定方法 === | |||
# 含有 <math>n</math> 个元素的集合有 <math>2^n</math> 个子集; | |||
# 含有 <math>n</math> 个元素的集合有 <math>(2^n-1)</math> 个真子集; | |||
# 含有 <math>n</math> 个元素的集合有 <math>(2^n-1)</math> 个非空子集; | |||
# 含有 <math>n</math> 个元素的集合有 <math>(2^n-2)</math> 个非空真子集. | |||
== 补集 == | |||
<math>\complement_U A</math> | |||
设<math>U</math>为全集(包含研究问题中涉及的所有元素的集合),集合<math>A</math>是<math>U</math>的子集,则由<math>U</math>中所有不属于<math>A</math>的元素组成的集合,称为集合<math>A</math>相对于全集<math>U</math>的'''补集''',记作<math>\complement_U A</math>(读作“<math>A</math>在<math>U</math>中的补集”)。 | |||
'''符号表示''':<math>\complement_U A = \{x | x \in U \text{且} x \notin A\}</math> | |||
'''性质''': | |||
* <math>A \cup \complement_U A = U</math>(集合<math>A</math>与其补集的并集为全集) | |||
* <math>A \cap \complement_U A = \emptyset</math>(集合<math>A</math>与其补集的交集为空集) | |||
* <math>\complement_U (\complement_U A) = A</math>(补集的补集是集合本身) | |||
'''示例''': | |||
设全集<math>U = \{1, 2, 3, 4, 5\}</math>,集合<math>A = \{1, 3, 5\}</math>,则<math>\complement_U A = \{2, 4\}</math>。 | |||
[[category: | [[category:代数]] | ||
2025年8月24日 (日) 22:12的最新版本
把研究的对象集在一起构成集合.
- 有有限个元素:有限集;
- 有无限个元素:无限集.
空集
不含元素的集合:
空集也是有限集.
元素和集合的关系
属于:
不属于:
集合中元素的三个特征
- 确定性:给定的集合,它的元素必须是确定的. 也就是说,给定一个集合,那么任何一个元素是否存在这一个集合中就确定了.
- 互异型:一个给定集合中的元素是互不相同的. 也就是说,集合中的元素是不重复出现的.
- 无序性:给定集合中的元素是不分先后的,没有顺序的.
数集
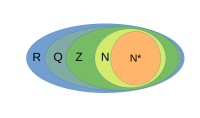
数学里最常用的集合是各种数的集合,简称数集。
示例
- 所有正整数组成的集合称为正整数集,记作 , 或
- 所有负整数组成的集合称为负整数集,记作
- 全体自然数组成的集合称为自然数集,记作
- 全体整数组成的集合称为整数集,记作
- 全体有理数组成的集合称为有理数集,记作
- 全体实数组成的集合称为实数集,记作
集合的表示方法
列举法
把集合中的所有元素一一列举出来,并用花括号“”括起来表示集合的方法叫做列举法.
注意事项:
- 元素与元素之间必须用“”隔开.
- 集合中的元素可以是任何事物.
- 集合中的元素不能重复.
示例:
一元二次方程 的解集为:.
描述法
一般地,设 A 表示一个集合,把集合 A 中所有具有共同特征 P(x) 的元素 x 所组成的集合表示为 ,这种表示方法称为描述法.
注意事项:
- 写清楚集合中元素的符号. 如数或点等.
- 不能出现未被说明的字母.
示例:
奇数集:.
偶数集:.
子集
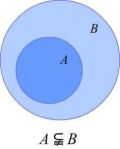
如果集合 的每一个元素都是集合 的元素,就称 是 的一个子集.
记作 (读作:A 包含于 B)或 (B 包含 A).
如果 并且 ,就说这两个集合相等,记作:.
如果 但是 ,就说 A 是 B 的真子集,记作:,读作:A 真包含于 B. 例如,.
包含关系还有传递性:
- 若 ,,则 ;
- 若 ,,则 ;
等等.
有限集的子集个数的确定方法
- 含有 个元素的集合有 个子集;
- 含有 个元素的集合有 个真子集;
- 含有 个元素的集合有 个非空子集;
- 含有 个元素的集合有 个非空真子集.
补集
设为全集(包含研究问题中涉及的所有元素的集合),集合是的子集,则由中所有不属于的元素组成的集合,称为集合相对于全集的补集,记作(读作“在中的补集”)。
符号表示:
性质:
- (集合与其补集的并集为全集)
- (集合与其补集的交集为空集)
- (补集的补集是集合本身)
示例: 设全集,集合,则。
